If the angle is unknown, but the lengths of the opposite and adjacent side in a right-angled triangle are known, then the tangent can be calculated from these two measurements.
Our tangent calculator accepts input in degrees or radians, so assuming the angle is known, just type it in and press 'calculate'. How to calculate the tangent of an angle? It is useful for finding an angle x when tan(x) is known.
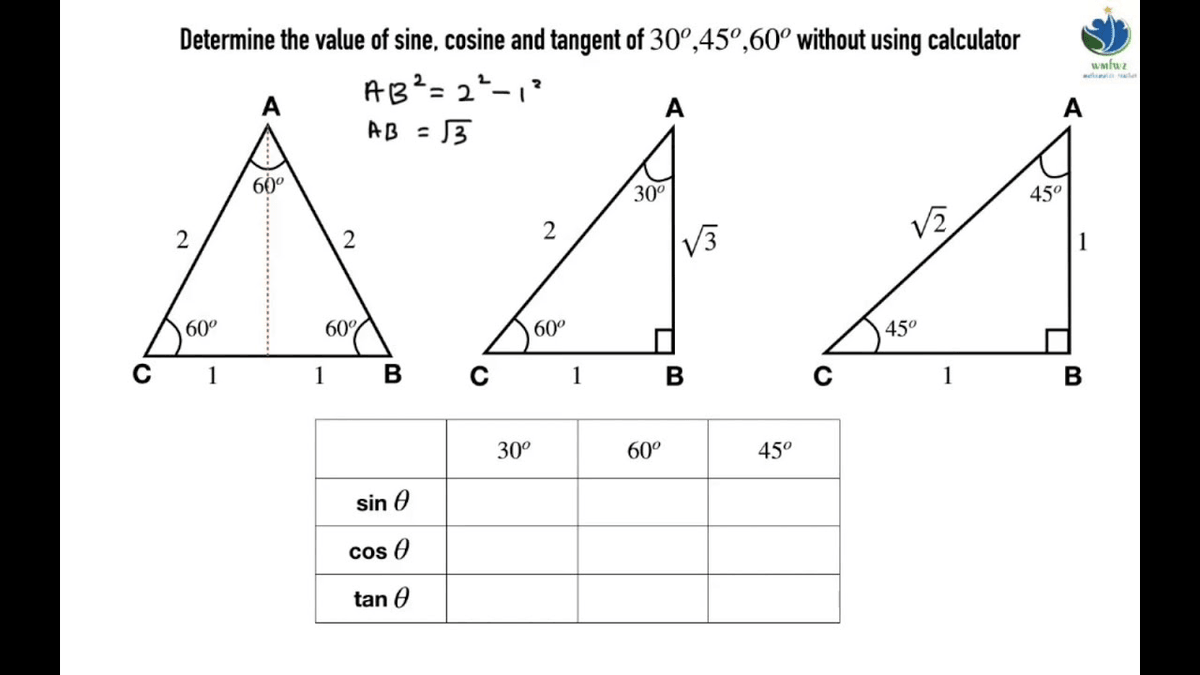
The inverse of the tangent is the arctangent function: arctan(x). The reciprocal of tangent is the cotangent: cot(x), sometimes written as cotan(x), which is the ratio of the length of the adjacent side to the length of the side opposite to the angle. Following from the definition, the function results in an undefined value at certain angles, like 90°, 270°, 460°, and so on. A tangent of an angle α is also equal to the ratio between its sine and cosine, so tanα = sinα / cosα. In the graph above, tan(α) = a/b and tan(β) = b/a. It is called 'tangent' since it can be represented as a line segment tangent to a circle. The tangent is a trigonometric function, defined as the ratio of the length of the side opposite to the angle to the length of the adjacent side, in a right-angled triangle.